This lab consist of creating a real image from a lens and a object projection. By adjusting distances for the object to the lens, a relationship can be studied between image distance, focal length, object distance and magnification.
The setup consisted of a paper screen, a light source, a ring stand, a clamp, a magnifying glass, a screen, and a meter stick. The light source was used to project an image through the magnifying glass (lens) and an then the screen was used to display the resulting image. By adjusting where the magnifying glass was, the object distance, image distance and image height could be changed.
 | |
| The object screen and light source used as a makeshift projector. |
 |
| Object image on the screen resulting from the lens converging light rays. |
The first task was to determine the focal length of a magnifying glass (lens) that was used in the experiment. The focal length was obtained by measuring the distance from the magnifying glass to the point where light was being focused. The focal length of the lens used is 26.0 cm.
The following table consist of a given object distance/height and the resulting image distance/height, All uncertainty for the measurements is the same since the same meter stick was used for all the measurements. A +/- 0.5 cm can be applied to all measurements made in centimeters. This will be addressed in the graphical analysis with error bars.
| Object Distance (cm) | Image Distance (cm) |
| 130 | 31.8 |
| 104 | 33.4 |
| 78 | 38.4 |
| 52 | 50.6 |
| 39 | 64 |
| Object Height (cm) | Image Height (cm) | Magnification | Type of Image |
| 3.3 | 0.85 | 0.24 | Real/Inv |
| 3.3 | 0.9 | 0.27 | Real/Inv |
| 3.3 | 1.5 | 0.45 | Real/Inv |
| 3.3 | 3.25 | 0.98 | Real/Inv |
| 3.3 | 6.3 | 1.9 | Real/Inv |
The following graph is the negative inverse of object distance vs. inverse image distance. The small blue cross marks that appear on the graph is the uncertainty bars for the given data points.
By interpolating the linear fit of this inverse graph, a conclusion can be reached that this data verifies the thin lens equation. The y-intercept is 0.03816 1/cm. If the inverse is take of that value, the result is 26.2 nm. This value is with 0.77% difference of our measured value for focal length of the magnifying glass. The slope is unit-less and when the inverse of the slope is taken it equals 1.10. This is 10% different from the value of the index of refraction of air. The thin lens equation is
By rearranging the equation to have the inverse of object distance(1/s) as the dependent variable and the negative inverse image distance(-1/s') to be the independent variable, the relationship that is supported by the graph can be seen.
This shows the inverse focal length to be the y-intercept and the slope to be one. The data in this lab successfully verifies this relationship through graphical interpolation.

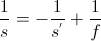
0 comments:
Post a Comment