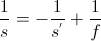General Relativity: Space Time Dilation

Modules were completed at Pearson's physics module website for sections 17.1 and 17.2. The following are screenshots of corresponding answers and models.




17.1

Answers to 17.1

Answers to 17.1 continued.

Screen shot of light clock model.

17.2

Answers to 17.2

Screen shot of length dilation model.

Programming Tutorial: Computational Model for Solar Cells

These are a series of programs that model solar cell reaction (current over power incident on the surface of the cell) vs. wavelength. The three different models fall into separate categories. The first category, completely theoretical, depicts a model solely based off of mathematical predictions. The second model, for manufactured cells, depicts what the reaction of manufactured silicon cells are. The third model, derived from our data, shows the reaction our cells had.


Completely Theoretical:

Picture of Graph for response vs wavelength. Units are in I/W and nm.

Picture of code from the above model.

Actual for Manufactured Cells:

Picture of Graph for response vs wavelength. Units are in I/W and nm.

Picture of code from the above model.

Picture of code from the above model.

Picture of code from the above model.

Picture of code from the above model.

Our Cells:

Picture of Graph for response vs wavelength. Units are in I/W and nm.

Picture of code from the above model.

Diffraction: Measuring CD Groove Size.

With a monochromatic light source and a CD it is possible to create a diffraction pattern. If a diffraction pattern is created from incident light on a CD surface, then the groove thickness in the CD can be measured. In this lab a red laser and a CD was used to create a diffraction pattern.  By projecting the pattern on to a screen and measuring the appropriate geometry, the value of groove thickness was obtained.

Image of CD surface depicting grooves and pits.

Diffraction in action! Neat!

Diffraction pattern created by CD.

The dots on the whiteboard correspond to intensity maxima. The order of the maxima are denoted and the geometry used is show in the triangle.

The distance measured from the CD and the screen is denoted by L in the above image. The distance from maximum to maximum was measured and denoted by X in the above image. From the geometry theta was calculated to be 1.46 degrees. The equation used to find the length of CD grooves was:

where m is 1 and d is the groove thickness. Its worth noting that the uncertainty in the geometric measurements can be disregarded. The uncertainty of 0.05 cm to the maxima measurements and the measurement from the screen to the CD is relatively small in comparison to the actual measurements. The actual thickness of data tracks on a given CD is 740 nm.


When the calculations are done the calculated value for thickness is 16811 nm. This error is due to how the experiment was treated. Theta was measured incorrectly. If theta was less than one a small angle approximation could be used resulting in a small multiple of wavelength. For example (670/.90)=1.11*670=740.  This leads to the conclusion that the geometry was incorrectly measured.

Light Interference: Measuring a Human Hair

     The purpose of this lab is to measure the thickness of a human hair in two different ways then compare the values. The first method of measuring the human hair will involve treating the human hair like a double slit screen that produces light interference. The second method will involve a traveling microscope: this method will be used to compare the thickness from method one.


     The setup involved using a red laser that was incident directly on a taut human hair. A screen was placed several meters away from the hair. The result was a pattern of light and dark fringes. By using the equation

it will be possible to obtain a reliable value for the thickness of the hair.

The bright and dark fringes projected onto the screen.

Fringe pattern denoted by dots followed with measurements

     The distance from the hair to the screen was 6.049 meters. The wavelength of the laser is estimated to be between 620-670 nanometers. Theta for m = 1 can be calculated through trigonometry. Theta is equal to the inverse tangent of 6.6 cm over 604.9 cm. This calculation results in theta being 0.625 degrees. Using 645 nm for wavelength, 0.625 degrees for theta and m = 1, the calculated value for d is 59130 nm which is equal to .059130 mm.


     The second method, the use of a traveling microscope to measure the hair thickness, resulted in a thickness of 0.1 mm +/- 0.05 mm.


     The two values fall within a reasonable range for hair thickness (provided by the professor: 1.8x10^-1 to 1.7x10^-2). The calculated value from the first method falls within the range of uncertainty of the second method. However, both of these methods have redeeming qualities and pit falls; consequently, this leads to both measurements being unreliable.  The first method uses exaggerated distances such as the screen being 6.049 meters away to overcome some uncertainties and errors in the experiment. The draw back to method one that makes it unreliable is the clarity of the interference pattern and the laser being directly incident on the strand of hair. Since those two factors are difficult to overcome without more of a time investment and a more secure apparatus for the laser/hair, it can be concluded the resulting value for hair thickness is unreliable. The advantage of method two is the ability to resolve the hair in a microscope and a sliding scale that can be moved with the microscope. The only disadvantage to the sliding microscope is the size of the sliding scale. Since the hair used in this lab was relatively fine, the traveling microscope had too large of a scale to measure the hair thickness without a large uncertainty. So while the two values fall within excepted range of hair thickness, this lab was unable to resolve absolute thickness of the studied hair sample.

Geometric Optics: Objects, Images, and Lenses

     This lab consist of creating a real image from a lens and a object projection. By adjusting distances for the object to the lens, a relationship can be studied between image distance, focal length, object distance and magnification. 

     The setup consisted of a paper screen, a light source, a ring stand, a clamp, a magnifying glass, a screen, and a meter stick. The light source was used to project an image through the magnifying glass (lens) and an then the screen was used to display the resulting image. By adjusting where the magnifying glass was, the object distance, image distance and image height could be changed. 

The object screen and light source used as a makeshift projector.

Object image on the screen resulting from the lens converging light rays.

     The first task was to determine the focal length of a magnifying glass (lens) that was used in the experiment. The focal length was obtained by measuring the distance from the magnifying glass to the point where light was being focused. The focal length of the lens used is 26.0 cm.


     The following table consist of a given object distance/height and the resulting image distance/height, All uncertainty for the measurements is the same since the same meter stick was used for all the measurements. A +/- 0.5 cm can be applied to all measurements made in centimeters. This will be addressed in the graphical analysis with error bars.

Object Distance (cm)	Image Distance (cm)
130	31.8
104	33.4
78	38.4
52	50.6
39	64

Object Height (cm)	Image Height (cm)	Magnification	Type of Image
3.3	0.85	0.24	Real/Inv
3.3	0.9	0.27	Real/Inv
3.3	1.5	0.45	Real/Inv
3.3	3.25	0.98	Real/Inv
3.3	6.3	1.9	Real/Inv

     The following graph is the negative inverse of object distance vs. inverse image distance. The small blue cross marks that appear on the graph is the uncertainty bars for the given data points.




     By interpolating the linear fit of this inverse graph, a conclusion can be reached that this data verifies the thin lens equation. The y-intercept is 0.03816 1/cm. If the inverse is take of that value, the result is 26.2 nm. This value is with 0.77% difference of our measured value for focal length of the magnifying glass. The slope is unit-less and when the inverse of the slope is taken it equals 1.10. This is 10% different from the value of the index of refraction of air. The thin lens equation is 

     By rearranging the equation to have the inverse of object distance(1/s) as the dependent variable and the negative inverse image distance(-1/s') to be the independent variable, the relationship that is supported by the graph can be seen.

     This shows the inverse focal length to be the y-intercept and the slope to be one. The data in this lab successfully verifies this relationship through graphical interpolation.

Optics: Concave and Convex Mirror Lab

The purpose of this lab is to explore the properties of convex and concave mirrors. This lab will consist of observing an object in either a convex or concave mirror; then, the object will be moved from it's original position and resulting in a change in the image of the object in the mirror. 

Image of my hand holding a nail in a convex mirror.

The first case examined is the nail image in the convex mirror.

Observations:

• The image is upright.
• The image is located behind the mirror.
• The image increases in size as the object distance to the mirror decreases.
• The light that would pass through the radius of curvature reflects back at the source.
• Light that is incident on the mirror reflects off the mirror in such a way where if the reflected ray is traced past the mirror the ray would pass through the focal point.
• The magnification of the object is equal to the ratio of image height and object height. 

The second case examined is the nail image in the concave mirror.

Observations:

• The image is inverted.
• The image is larger than the object.
• The image is in front of the mirror.
• The image size increases as object distance approaches focal length, past the focal length the object shrinks in size.
• If the object was within the focal length, the object was upright. 
• If the object was past the focal length it was inverted.
• The magnification of the object is equal to the ratio of image height and object height.
• Light rays that pass through the radius of curvature reflect back to the source.
• Light rays that pass through the focal length reflect back out parallel to the optical access.
• Light rays that are parallel to the optical axis reflect and pass through the focal point. 

Conclusion:

In the convex mirror, the image formed was virtual and located behind the mirror. The image formed in the concave mirror is a real image when the object is located outside the focal length. If the object is inside the focal length of a concave mirror, the image forms behind the mirror and the image is virtual. Both convex and concave mirror images can be located by the intersection of rays, or better known as ray tracing. For both convex and concave mirrors, the magnification is equal to the ratio of image height and object height.