The purpose of this lab is to explore Archimedes principle and fluid statics. Archimedes' principle states that an object immersed in a liquid will experience a buoyant force which is equal to the weight of the volume of displaced liquid. In essence there will exist now an apparent weight of the object and an actual weight where the apparent weight is equal to the difference in the actual weight and buoyant force.
Archimedes' Principle:
In this lab, the goal is to measure the buoyant force with three different methods. Each method will take advantage of Archimedes' principle in a different way. By using different methods to measure buoyant force, it will be possible to verify Archimedes' principle.
The equipment used for this lab is as follows.
- Force Probe
- String
- Overflow tray
- Beaker
- Mass
- Calipers
- Ruler
The three methods used to measure buoyant force are :
- Underwater Weighing
- Displaced Fluid
- Volume of Object
The underwater weighing method consists of measuring the weight of the mass outside of the water followed by measuring the weight of the mass completely submerged. In theory, since the apparent weight is equal to the difference of the buoyant force and actual weight, it is possible to obtain the buoyant force from the difference of actual weight and apparent weight. The values for actual and apparent weight are as follows:
Actual Weight: 0.94 N +/- 0.02N
Apparent Weight: 0.81 N +/-0.02N
The uncertainty is due to spikes and dips from measuring with the force probe over time. The values recorded were averages and the uncertainty is the range over which the values occurred. After applying the principle discussed to obtain buoyant force, the result is:
Buoyant Force = 0.13N +/- 0.04N
Method #2 : Displaced Fluid
The displaced fluid method consists of submerging a mass in a beaker that is completely full of water. As the mass descends into the fluid, water will overflow from the top. The overflow is caught then weighed. In principle the weight of the displaced fluid is equal to the buoyant force. A beaker filled with water was placed in a overflow tray. Then, a mass was submerged in the full beaker. The over flow was collected into a beaker which has a known mass. The beaker with the water was weighed.
Mass of Empty Beaker = 0.0963 kg
Mass of Empty Beaker + Mass of Overflow Liquid = 0.1599 kg
Mass of Overflow Liquid = 0.0636 kg
Weight of Overflow Liquid = 0.624 N
The weight of the over flow liquid is the same as the weight of the displaced fluid: the value 0.0624 N is the buoyant forced measured for method #2. In comparison to the first result, buoyant force is greatly different in the first method versus the second method. This will be addressed later in the lab
Method #3: Volume of the Object
The volume of a completely submerged mass is equal to the total displaced volume of the fluid it's submerged in. By measuring the change in volume, it is possible to find the volume of displaced water. In turn, if the volume of displaced water is know it is easy to obtain buoyant force. A beaker was filled with some water. The cross sectional area of the beaker was measured along with the initial height of the water: the result of those two measurements was the initial volume. Then, the mass used in parts 1 and 2 was completely submerged. This led to a chance in volume. The height of the water level was measured again to find the new volume. The difference between the initial volume wand the final volume is equal to the volume of the mass and the displaced fluid.
Initial Volume = 0.000178 cubic meters
Final Volume = 0.000250 cubic meters
Change in Volume = 0.0000725 cubic meters
Weight of Displaced Water = 0.725 N
The weight of the displaced water is equal to the buoyant force. This value is closed to method #2, but the difference between method #3 is large. This will be addressed at the end of the lab.
Summary-Questions
1)
The three difference values for buoyant force are as follows:
- Method #1 F = 0.13 N +/- 0.04N
- Method #2 F = 0.624 N
- Method #3 F = 0.725 N
The values from methods #2 and #3 are within an acceptable range of each other when you take into account the pitfalls of the method #2. Catching all the liquid overflow is difficult. The surface tension can capture some water that should have overflowed as well as water spilling out or sticking to other surfaces. Method #2 has a challenge of capturing the most overflow possible. It is easy to speculate that 100 N of water (roughly 10 grams) was lost on different surfaces or remained in the beaker. The alternative that the beaker was not completely full in method #2: this would also easily lead to a 10 gram discrepancy. The issue with Method #1 being drastically different from the other methods is puzzling. It was a simple process; essentially the mass was weighed in and out of water. The difference between those values should be the buoyant force. Looking back at the picture displaced earlier in the report with the equipment, the mass used was a relatively large sphere. The sphere was large enough to cause suction effects and this could throw the submerged weight measurement off. It might have been possible that the mass was simple to heavy for the settings on the force probe. The probe was set to a +/- 10 N limit and the mass used in this experiment bordered on one kilogram. I would speculate that method #1 and #3 should be relatively the same while method #2 would maintain a higher level of discrepancy.
2)
Method #3 was the most accurate. I believe this method is the most accurate because it fell on easily measurable quantities that could be used with Archimedes' principle. The instruments used in the process are fairly accurate (ruler and calipers). The principle was that the change in volume was the displaced volume. The change in volume was easily and accurately measured. Method #2 had pitfalls in correctly handling overflow, which is quite difficult to raise to the level of accuracy that is obtainable in method #3. Method #1 also has pitfalls such as the mass touching any surface. Method #3 has no mentionable pitfalls other than uncertainty with the ruler and calipers.
3)
In Method #1, if the mass had touched the bottom of the container, it would have made the apparent weight seem less and in turn made the calculated buoyant force larger. Essentially the buoyant force would be getting credit for the normal force as well. By looking at the equation you would get:
F + T + N = W
Where F = Buoyant Force
T = Tension = Apparent Weight
N = Normal Force
W = Weight
Rearrange
T = W - (F + N)
It can be seen than the apparent weight will be less with a normal force. If the person measuring is unaware of that normal force they would come to the conclusion the buoyant force is much stronger that it actually is.

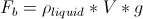

0 comments:
Post a Comment